Usted está aquí
Investigación matemática como estrategia pedagógica
Investigación matemática: una estrategia pedagógica en el aula
Autor
Martha Lucía Acosta y Anneris Joya Vega
Profesoras Departamento de Matemáticas Gimnasio Campestre
[email protected], [email protected]
“Mathematics is a living subject which seeks to understand patterns that permeate both the world around us and the mind within us”
Schoenfeld (1992)
Resumen
Este artículo presenta algunas perspectivas teóricas acerca de la investigación como estrategia metodológica en el aula de matemáticas y su relación con el pro- ceso de solución de problemas. Adicionalmente, hace una reflexión acerca de las ventajas del uso de la investigación en el aula de matemáticas y la metodología que se podría implementar para promover las competencias que conforman el Modelo Pedagógico del Gimnasio Campestre.
Introducción
Son varias las propuestas metodológicas que han tenido como objetivo usar la investigación para dinamizar procesos escolares y generar un espíritu científico en los estudiantes. Mejía y Manjarrés (2009) reseñan varios autores que han trabajado diferentes metodologías de enseñanza enfocadas en la investigación; entre ellos se encuentran Garrison y Anderson, Wills, Short, et. al., Shagoury, et, al, Gil Pérez, Lipman y Sharp, Liberman y Miller, Lederman, Sharpak.
En particular en matemáticas, desde su naturaleza misma y su filosofía, la investigación es considerada una estrategia fundamental para la producción de conocimiento. Schoenfeld (1992) define la matemática como:
Una actividad inherentemente social en la cual una comunidad de expertos entrenados (científicos matemáticos) se interesa en la ciencia de los patrones -ensayos sistemáticos basados en observación, estudio, y experimentación-, para determinar la naturaleza o los principios de las regularidades en sistemas definidos axiomática y teóricamente (matemáticas puras) o modelos de sistemas abstraídos de objetos del mundo real (matemáticas aplicadas).
Los estudios en filosofía de las matemáticas de Ernest (1991), Davis y Hersh (1980), Lakatos (1976) y Tymoczkco (1986) (citados por Ponte, et. al., 1998) han centrado su atención en la actividad matemática y específicamente en el proceso investigativo que tiene lugar durante la creación de un nuevo conocimiento matemático. Ponte, et.al. (1998) afirman que “existe un acuerdo general entre los educadores en el que aprender matemáticas incluye de manera fundamental, hacer matemáticas” y por su parte, Poincaré afirma que (1908/1974/1987) “hacer matemáticas es primero que todo hacer investigación matemática.”
Para Ponte et al. (1998), el proceso de investigación matemática en el aula de clase parte de dos objetivos. El primer objetivo consiste en comprender una idea matemática, un concepto o un pro- ceso; el segundo consiste en organizar y explicar un conjunto de datos en términos matemáticos. Según estos autores, el proceso de investigación puede darse a través de los siguientes pasos:
- Formular preguntas que sean razonables
- Proponer conjeturas
- Recolectar datos para justificar las conjeturas establecidas o generar nuevas conjeturas
- Realizar pruebas formales fundamentadas en argumentos sólidos que permitan confirmar las conjeturas, redefinirlas o, por el contrario, rechazarlas. Durante este proceso, pueden establecerse nuevas preguntas que conduzcan a nuevas investigaciones.

Acerca de las preguntas, Wagensberg (citado por Mejía, 2007) señala que hay dos posiciones frente a la pregunta:
En una primera actitud el mundo es visto como un mundo de preguntas y mi tarea es buscar las respuestas correctas. Allí la preocupación es la causalidad y la finalidad de lo que acontece… Una segunda actitud es aquella en la cual la pregunta busca la inteligibilidad de lo que ocurre. Ésta conduce necesariamente a la investigación, ya que si vemos la historia de la ciencia, sus adelantos, está marcada por ser respuesta a buenas preguntas. (p.27)
Investigación como estrategia pedagógica
Aunque existe una nueva tendencia de algunos autores a considerar la investigación como una poderosa estrategia en el aula de matemáticas (Yeo y Yeap 2009, Quinnel, Ponte, et al., entre otros), no hay una única posición frente al tipo de preguntas, problemas o tareas que pueden conducir a dicha investigación frente a la relación entre ella y solución de problemas. Pocos educadores hablan de la investigación matemática como una estrategia para la solución de problemas, pues la asumen como una actividad abierta que incluye, como primera etapa, la proposición del problema a partir de los datos dados (Orton y Frobisher, citado por Yeo y Yeap, 2009). En este sentido, podría entenderse que los problemas cerrados que generalmente se proponen en el aula de matemáticas no se pueden resolver mediante la investigación. Sin embargo, Yeo y Yeap (2009) argumentan que la investigación matemática también puede ser un medio para resolver este tipo de problemas.
Para abordar el argumento de Yeo y Yeap (2009), a continuación se caracterizan, por un lado, la solución de problemas cerrados y por el otro, la actividad investigativa abierta en relación con los procesos cognitivos que requiere cada una.
Solución de problemas
En primer lugar, Yeo y Yeap (2009) definen un problema como una tarea propuesta por el profesor que no tiene una solución inmediata para el estudiante. Es decir, no puede aplicar un procedimiento ya conocido que le permita su solución (Lester, 1980, citado por Yeo y Yeap, 2009) y requiere de un esfuerzo creativo de aplicación de estrategias y un nivel superior de pensamiento para abordar su solución (Reys, Lindquist, Lambdin, Smith y Suydam, citado por Yeo y Yeap, 2009).
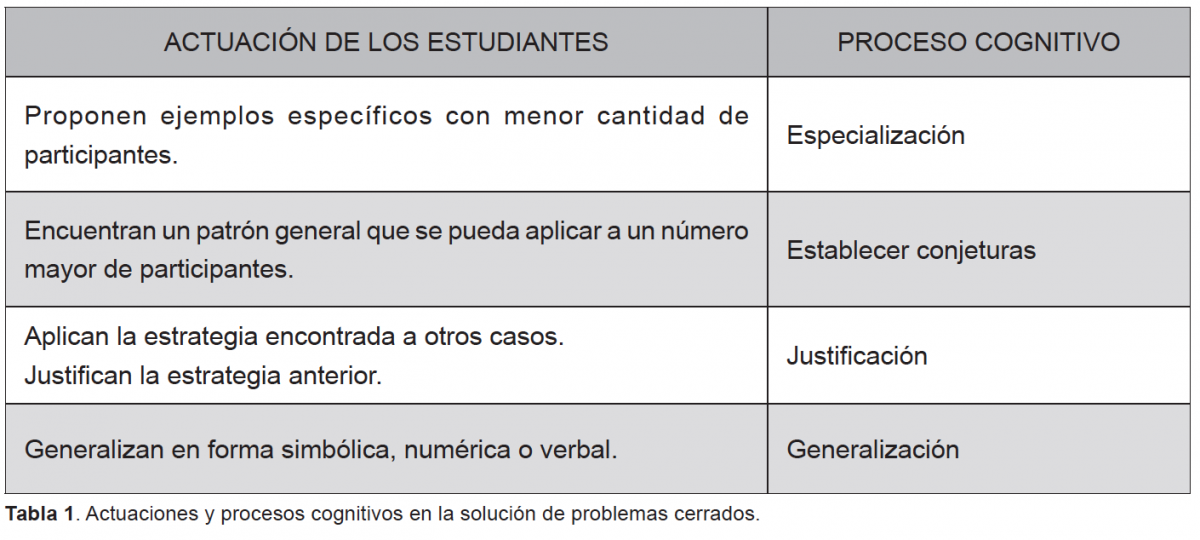
Los investigadores Mason, Burton y Stacey (1985) identificaron, a partir de sus investigaciones, cuatro procesos de pensamiento matemático en la solución de problemas matemáticos cerrados: especialización, establecimiento de conjeturas, justificación y generalización.
A continuación se muestra un ejemplo de solución de problemas cerrados.
Tarea 1. En un taller, cada uno de los 70 participantes da la mano para saludar a los demás, una sola vez. Encontrar el número total de saludos.
Al aplicar esta tarea a estudiantes del Gimnasio Campestre (Figura 1 y Figura 2) se pudo establecer una relación entre sus actuaciones y los procesos cognitivos establecidos por Mason, Burton y Stacey (1985) para la solución de problemas cerrados. (Tabla 1)
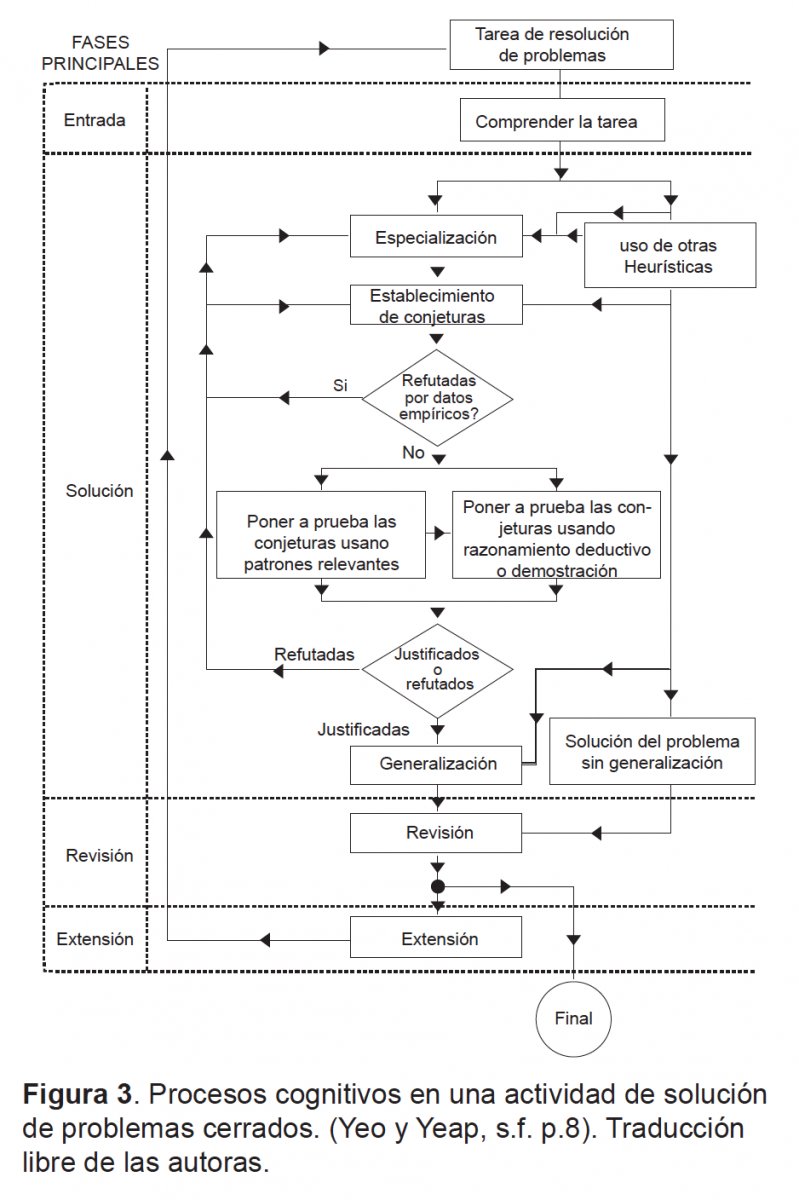
Adicionalmente, Yeo y Yeap (2009) proponen el siguiente modelo de interacción de los procesos cognitivos en una actividad de solución de problemas cerrados. Este modelo, incluye cuatro fases: entrada, ataque, revisión y extensión (Figura 4).

 Actividad investigativa abierta
Actividad investigativa abierta
Yeo y Yeap (2009) establecen una diferencia entre la investigación como tarea y como actividad. De acuerdo con Christiansen y Walther (1986), citado por Yeo y Yeap (2009), una tarea se refiere al enunciado propuesto por el profesor, mientras que la actividad la constituyen todas las acciones que realiza el estudiante para desarrollar la tarea propuesta.
Adicionalmente, estos autores establecen una diferencia entre la investigación como actividad y la investigación como proceso. En matemáticas, el profesor puede proponer tareas investigativas abiertas que requieren por parte de los estudiantes tanto del planteamiento un problema, como de la solución del mismo. Sin embargo, los autores consideran que el proceso de investigación para este tipo de tareas inicia una vez propuesto el problema por los estudiantes y establecen el proceso de investigación como una etapa de la actividad investigativa abierta.
A continuación, se muestra un ejemplo de tarea investigativa abierta en la que Yeo y Yeap (2009) demuestran que es una actividad en la que los estudiantes deben proponer su propio problema y resolverlo.
Tarea 2: Números cordiales
Números cordiales son números naturales que se pueden expresar como la suma de dos o más números naturales consecutivos. Por ejemplo:
9 = 2 + 3 + 4 = 4 + 5
11 = 5 + 6
18 = 3 + 4 + 5 + 6
Investigue.
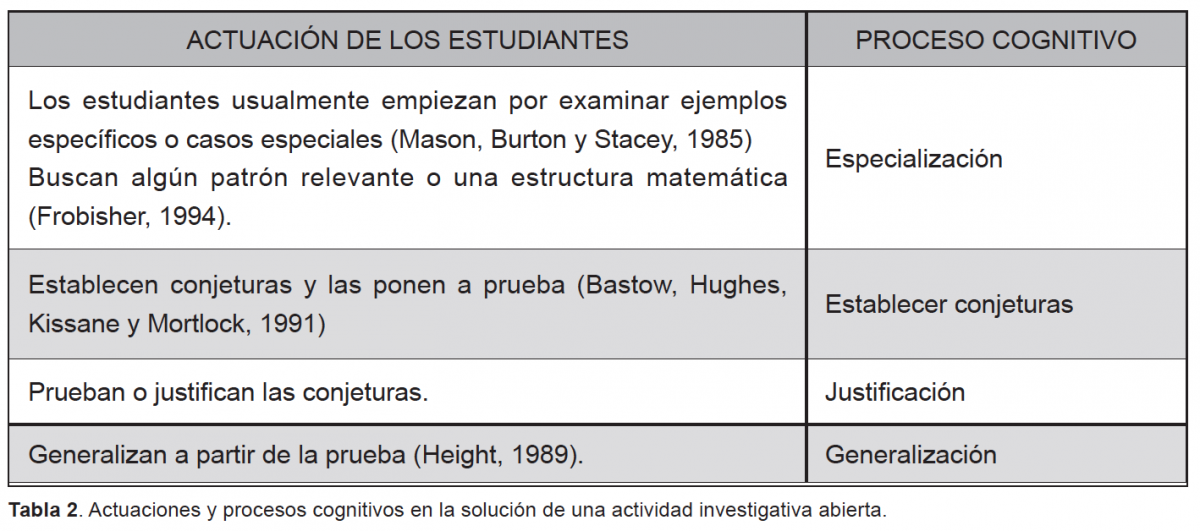
 Yeo y Yeap (2009) observaron y describieron las actuaciones de un grupo de estudiantes durante el desarrollo de esta actividad investigativa. Encontraron que los estudiantes inicialmente examinan ejemplos o casos especiales; luego, como resultado de la primera etapa de búsqueda de patrones o estructuras, los estudiantes formulan y prueban conjeturas para, finalmente, justificar y probarlas. Los autores relacionaron estas actuaciones de los estudiantes con los cuatro procesos de pensamiento matemático propuestos por los investigadores Mason, Burton y Stacey (1985) en la solución de problemas matemáticos cerrados: especialización, establecimiento de conjeturas, justificación y generalización (Tabla 2).
Yeo y Yeap (2009) observaron y describieron las actuaciones de un grupo de estudiantes durante el desarrollo de esta actividad investigativa. Encontraron que los estudiantes inicialmente examinan ejemplos o casos especiales; luego, como resultado de la primera etapa de búsqueda de patrones o estructuras, los estudiantes formulan y prueban conjeturas para, finalmente, justificar y probarlas. Los autores relacionaron estas actuaciones de los estudiantes con los cuatro procesos de pensamiento matemático propuestos por los investigadores Mason, Burton y Stacey (1985) en la solución de problemas matemáticos cerrados: especialización, establecimiento de conjeturas, justificación y generalización (Tabla 2).
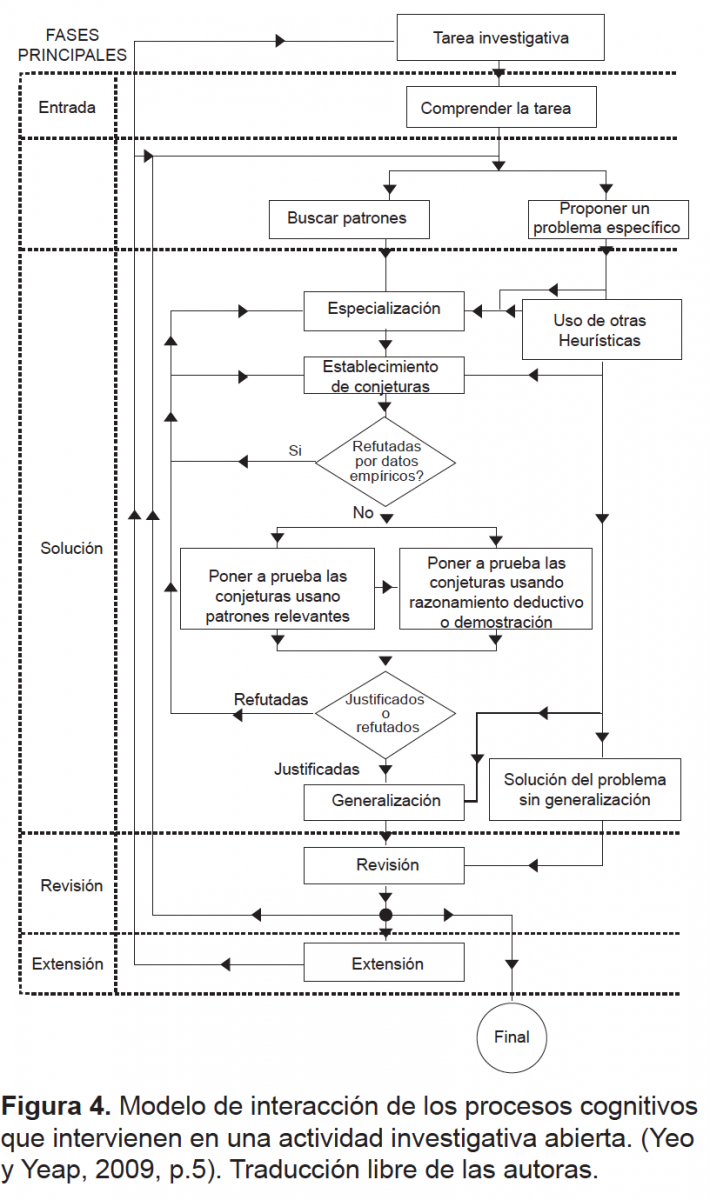
En la figura 4 se muestra el modelo de interacción de los procesos cognitivos que intervienen en una actividad investigativa abierta, propuesto por Yeo y Yeap (2009). En este modelo intervienen cinco fases: entrada, establecimiento de la meta, ataque, revisión y extensión.
Al comparar los esquemas de la figura 3 y la figura 4, se puede observar la relación entre una actividad investigativa abierta y una actividad de solución de problemas cerrados. Al caracterizar la investigación matemática como un proceso que incluye los procesos cognitivos especialización, establecimiento de conjeturas, justificación y generalización (Yeo y Yeap, 2009), la investigación matemática puede darse tanto en una actividad investigativa abierta como en una actividad de solución de problemas cerrados.
Conclusiones
Caracterizar la investigación matemática a partir de los procesos de pensamiento matemático de especialización, establecimiento de conjeturas, justificación y generalización, que se dan tanto en la solución de un problema matemático cerrado como en una actividad investigativa abierta, permite a los profesores tener una mayor claridad al diseñar una secuencia de actividades de enseñanza que promueva el desarrollo de estos procesos en los estudiantes. En este sentido, la investigación matemática se constituye en una estrategia pedagógica en el aula de matemáticas, que puede ser usada tanto en la solución de problemas cerrados, como en la solución de tareas investigativas abiertas.
Es importante reconocer el aporte del proceso de investigación para los estudiantes porque genera un ambiente similar al de una comunidad matemática, en la que el objetivo común es construir conocimiento matemático mediado por la interacción de los estudiantes, la comunicación y justificación de sus razonamientos y la confrontación constante de sus conjeturas y argumentaciones.
El rol del profesor en un ambiente en el que la investigación es una estrategia pedagógica en la clase de matemáticas se debe centrar en los siguientes aspectos:
- Su concepción acerca del aprendizaje de las matemáticas. Asumir que el aprendizaje se da mediante la actividad, la interacción y la reflexión.
- La selección de tareas orientadas no sólo a la práctica de hechos y procedimientos básicos, sino a la exploración y al desarrollo de competencias relacionadas con preguntarse, pensar, validar y corregir.
- La forma como genera espacios dentro de clase para negociar significados y el estilo de intervenciones que realiza para manejar la negociación de significado.
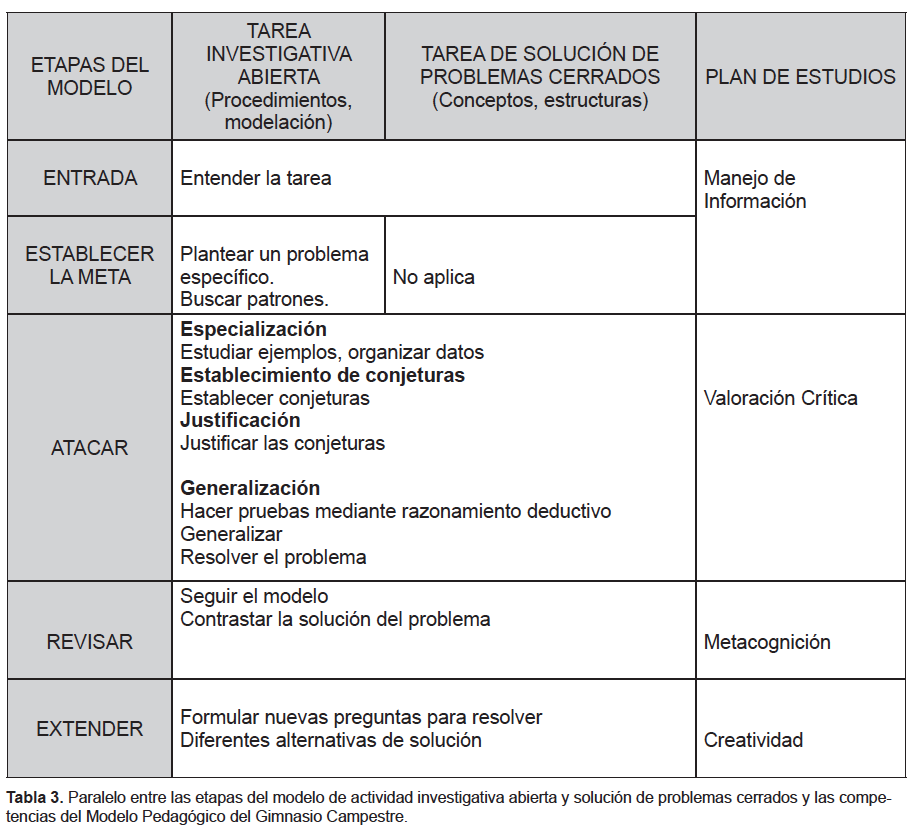
Los modelos de actividad investigativa abierta y de solución de problemas cerrados y la interacción de los procesos cognitivos de investigación matemática, que se dan en estos dos tipos de actividad, permiten una asociación entre la actividad matemática y las competencias del plan de estudios del Gimnasio Campestre. Seguir las etapas de los modelos presentados contribuye a la implementación del plan de estudios en cuanto se puede establecer un paralelo entre éstas y las competencias que se proponen en el Modelo Pedagógico (Tabla 3).
Referencias
Ernest, P. (1991). The philosophy of mathematics education. London: Palmer Press.
Mejía, M y Manjarrés M. (2009). Las pedagogías fundadas en la investigación. Búsquedas en la reconfiguración de la educación. Revista internacional Magisterio. Educación y pedagogía. No. 42. (Diciembre 2009- Enero 2010) 16-24.
Mejía, M. (2007) La pregunta: entre estrategia pedagógica y camino investigativo. Construyendo rutas de saber y conocimiento. Revista internacional Magisterio. Educación y pedagogía. No. 27, 26-30.
Ponte, J. P., Ferreira, C., Brunheira, L., Oliveira, H., y Varandas, J. M. (1998). Investigating mathematical investigations. In P. Abrantes, J. Porfirio, y M. Baía (Eds.) Setúbal: ESE de Setúbal. Les interactions dans la classe de mathématiques: Proceedings of the CIEAEM 49, 3-14.
Quinell, L. (2010). Why are mathematical investigation important? http://search.informit.com. au/documentSummary;dn=354660956542599;res= IELHSS. Recuperado el 23 de septiembre de 2013.
Schoenfeld, A.H. (1992). Learning to think mathe- matically: Problem solving, metacognition, and sensemaking in mathematics. In D. Grouws (Ed.), Handbook on Mathematics Teaching and Learning (334-370). New York: MacMillan
Yeo, J. y Yeap, B. (s f ). Characterising the cognitive processes in Mathematical Investigation http:// www.cimt.plymouth.ac.uk/journal/jbwyeo.pdf . Recuperado el 23 de septiembre de 2013.
Yeo, J. y Yeap, B. (2009). Mathematical investiga- tion: Task, process and activity. Tech. Rep ME2009-01. National Institute of Education, Nanyang
Este documento fue tomado de www.revistaelastrolabio.com
- 9575 lecturas






