Estrategias metacognitivas

El Modelo Pedagógico actual del Gimnasio Campestre, se fundamenta en cuatro competencias: gestión de la información, valoración crítica, creatividad y metacognición. Específicamente, la metacognición se define como el conjunto de conocimientos, habilidades y actitudes que el estudiante debe poner en práctica para el continuo autoexamen, autocontrol, autorregulación y autocorrección de su pensamiento. Uno de los descriptores asociados a esta competencia, está referido a “la capacidad de ser consciente de su propio avance en el proceso de tomar decisiones para solucionar problemas”.

Teniendo en cuenta la importancia que tiene la solución de problemas en la investigación en Didáctica de las Matemáticas, en el currículo colombiano y en el plan de estudios del Gimnasio Campestre, se realizó esta in- vestigación que busca elegir e implementar estrategias metacognitivas asociadas a la solución de problemas multiplicativos, que favorezcan la competencia metacognitiva de los estudiantes y hagan observables y evaluables las estrategias específicas usadas por los estudiantes.

Objetivos Generales

Implementar una estrategia general que contribuya al desarrollo de las  habilidades metacognitivas de los estudiantes, para resolver problemas multiplicativos, a través del estudio de las estrategias metacognitivas específicas que ellos usan en la solución de problemas multiplicativos, a partir de la estrategia general.

Marco teórico

Se identificaron tres aspectos que han sido estudiados desde la psicología y la Didác- tica de las Matemáticas: el concepto de metacognición en educación, las estrategias metacognitivas en la solución de problemas matemáticos y, las tipologías de problemas multiplicativos.

Metacognición en Educación

Flavell (1979) define la metacognición en el campo de la educación a partir de su relación con  los procesos involucrados en el aprendizaje académico: atención, comprensión, memoria, lectura, resolución de problemas y estrategias utilizadas por los aprendices eficientes para aprender a aprender.

Acorde con el problema de esta investigación, asumimos la postura teórica de Flavell (1979) quien define la metacognición como el conocimiento de los propios procesos cognoscitivos, de los resultados de esos procesos y de cualquier aspecto que se relacione con ellos; es decir, el aprendizaje de las propiedades relevantes de la información. Flavell (1979) distingue dos aspectos ligados a la metacognición: el conocimiento sobre los procesos cognitivos y la regulación de dichos procesos. El primer tipo de conocimiento es de naturaleza declarativa y se distinguen en éste tres categorías de conocimientos: sobre personas, sobre tareas y sobre estrategias. El segundo tipo de conocimiento se refiere al aspecto procedimental y permite encadenar de forma eficaz las acciones necesarias para alcanzar una meta; en este tipo de conocimiento se distinguen tres procesos que corresponden a tres fases en la solución de un problema, el de planificación, el de control y el de evaluación.

Estrategias metacognitivas  en la solución de problemas matemáticos

Flavell (1979) establece diferencias entre las estrategias cognitivas y las metacognitivas a partir de su finalidad; las estrategias cognitivas se aplican para hacer progresar una actividad, mientras que las metacognitivas tienen como función supervisar el proceso. Sin embargo, Hernández (2002) ha mostrado en sus estudios que estos dos tipos de estrategias interactúan durante la solución de un problema matemático.

Hernández (2002) señala que para resolver un problema matemático se pueden usar dos tipos de estrategias metacognitivas: las estrategias generales, que son técnicas que guían la solución de problemas en diferentes campos del conocimiento y las estrategias específicas, que se fundamentan en los esquemas, que corresponden a cada unidad de conocimiento matemático, las cuales contienen información que permiten clasificar un problema e identificar cómo resolverlo. Además Hernández (2002) afirma que un buen modelo de enseñanza de estrategias cognitivas y metacognitivas en la solución de problemas, debe por una parte, proveer una tipología de problemas asociados al conocimiento matemático, que proporcione las estrategias de solución correspondientes y por otra parte, incluir el desarrollo de estrategias metacognitivas que permitan utilizar adecuadamente los recursos y controlar y evaluar su ejecución.

La estrategia general propuesta por Polya (1945) para la solución de problemas con- templa cuatro fases: comprender el problema, concebir un plan, ejecutar el plan, examinar la solución obtenida. Los esquemas en los que se fundamentan las estrategias específicas contienen información sobre cómo y cuándo utilizar los conceptos, principios y fórmulas relacionadas con un dominio del conocimiento específico.

Tipología de problemas multiplicativos y estrategias de solución

Los Lineamientos curriculares (MEN, 1998) hacen referencia a la complejidad de la solución de problemas asociados a la estructura multiplicativa, con respecto a los asociados a la aditiva, puesto que en las situaciones multiplicativas se hace una correspondencia entre uno de los elementos de un conjunto y subconjuntos equivalentes de otro conjunto. Así mismo, proponen cuatro tipos de problemas asociados a la multiplicación: factor multiplicante, adición repetida, ra- zón y producto cartesiano y, dos tipos de problemas asociados a la división: repartir y agrupamiento o sustracción repetida.

De esta manera, para los problemas asociados a la multiplicación 4 x 5, tendríamos los siguientes tipos:

a. Factor multiplicante
Pablo tiene 4 cartas, Santiago tiene 5 veces más. ¿Cuántas cartas tiene Santiago?

b. Adición repetida
Pablo tomó 4 pastillas durante 5 días.
¿Cuántas pastillas tomó en total?

c. Razón
4 niños tienen 5 carritos cada uno, ¿cuántos carros tienen en total?

d. Producto cartesiano
Un carrito de juguete se fabrica en 4 tamaños diferentes y en 5 colores diferentes. ¿Cuántos carritos distintos se pueden comprar?

Por otra parte, los tipos de problemas asociados con la división 12÷4 son:

a. Repartir
Santiago tiene 12 carritos. Quiere colo- carlos en 4 hileras iguales. ¿Cuántos debía colocar en cada hilera?

b. Agrupamiento o sustracción repetida Santiago tiene 12 carritos. Quiere colo- carlos en hileras de  4. ¿Cuántas hileras puede hacer?

Materiales y métodos

Coherente con el problema de investigación consideramos que el enfoque metodológico cualitativo-interpretativo brinda los elementos necesarios para abordarlo. Como método de investigación elegimos el estudio de caso (Fragoso, 2004) puesto que sus características, particularista, descriptivo y heurístico, nos facilitan el logro de los objetivos de la investigación.

Dado que en este estudio analizamos las producciones escritas de los estudiantes, implementamos la técnica análisis de contenido usada para decodificar los mensajes tanto implícitos como explícitos presentados en diferentes documentos (Almenara & Loscertales, 2002).

Fases de la investigación

Las fases de esta investigación corresponden a las propuestas por Fragoso (2004) para un estudio de caso.

Familiarización con el objeto de estudio: revisamos investigaciones acerca de es- trategias metacognitivas en la solución de problemas multiplicativos, establecimos los elementos teóricos y prácticos que justifican el problema, y delimitamos claramente el problema y los objetivos.

Recolección de datos: Para la recolección de datos usamos como instrumentos algunas de las producciones de los estudiantes en clase:

• Instrumento 1. Problema multiplicativo inicial.
• Instrumento 2. Problema multiplica- tivo con aplicación de la estrategia general.
• Instrumento 3. Taller de implemen- tación de la tipología de problemas multiplicativos.
• Instrumento 4. Evaluación sobre aplica- ción de estrategia general y tipología de problemas multiplicativos.
• Instrumento 5. Pregunta (aspecto de- clarativo) acerca de las estrategias de verificación.

Estrategias de análisis: establecimos un sistema categorial con base en el marco teórico, elegimos e implementamos una es- trategia general y una tipología de problemas multiplicativos, para finalmente, realizar el análisis de contenido de las producciones de los estudiantes en forma cualitativa.

Validación: realizamos una permanente triangulación entre las interpretaciones, el marco teórico  y el sistema categorial.

Sistema categorial

Para proponer la estrategia general en la solución de problemas multiplicativos, nos basamos por una parte, en los tres procesos propuestos por Flavell (1979) en el conocimiento procedimental, que corresponden a tres fases en la solución de un problema y en las etapas de la estrategia general propuesta por Polya (1945), procesos y fases que se relacionan en la Tabla1.

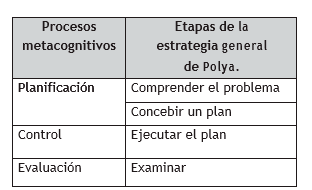
Tabla 1. Relación entre los procesos metacognitivos y las etapas de la estrategia general

La implementación de la estrategia general sirve como medio para que los estudiantes evidencien las estrategias específicas. Las estrategias específicas en la solución de problemas, corresponden a las acciones que realiza el estudiante frente a los  procesos metacognitivos de planificación, control y evaluación y, que están fundamentadas en la elección de los recursos cognitivos pertinentes. Como lo afirma López (s.f.), la metacognición en el aprendizaje está aso- ciada con “la toma de conciencia por parte del alumno acerca de lo que está sucediendo en su mente cuando enfrenta una tarea, de forma tal que el mismo estudiante pueda conocer y decidir acerca del mejor uso de sus recursos cognoscitivos”.

Para facilitar a los estudiantes, la elección apropiada de sus recursos cognitivos en la solución de problemas multiplicativos incluimos en el modelo de enseñanza, la tipología de problemas asociados a la multi- plicación y a la división (MEN, 1998) con las representaciones y procedimientos propios.

Para el análisis y posterior descripción de las estrategias metacognitivas específicas que usan los estudiantes, asumimos como categorías de análisis, los procesos metacognitivos en relación con las acciones que el estudiante evidencie en cada etapa de la solución de un problema.

Análisis de datos y resultados

Inicialmente, propusimos a todos los estudiantes de tercer grado resolver un problema multiplicativo para identificar las estrategias metacognitivas espontáneas que mostraban en el proceso de solución (Ilustraciones 1 y 2). Al analizar las soluciones propuestas por los estudiantes, observamos que el 72,22 % de los estudiantes, determinaron tres pasos en la solución: datos, operación y respuesta, pasos que son de carácter operativo y que no permiten observar procesos metacognitivos. Este resultado nos permitió identificar la necesidad de implementar un modelo de enseñanza que hiciera observable y por lo tanto evaluable, la competencia metacognitiva de los estudiantes frente a unas evidencias de desempeño, en la solución de problemas multiplicativos.

Ilustración 1. Ejemplo de solución en 3 pasos. Instrumento 1, Caso 4.

Con base en el análisis de las posturas teóricas en Didáctica de las Matemáticas

Ilustración 2. Ejemplo de solución que no muestra una estrategia general. Instrumento 1, Caso 4.

acerca de los procesos metacognitivos, la estrategia general de solución de problemas (Polya,1945) y los tipos de problemas mul- tiplicativos, logramos establecer unas rela- ciones que nos permitieron construir como resultado teórico, un modelo de enseñanza para la solución de problemas multiplicativos (Ilustración 3).

Ilustración 3. Modelo de enseñanza de solución de problemas.

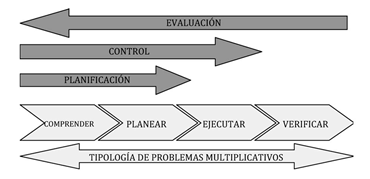
En el modelo establecimos una estrategia general con cuatro etapas: comprender, planear, ejecutar y verificar. Ésta permitió identificar las estrategias metacognitivas específicas, entendidas como las acciones que el estudiante realiza en cada una de las etapas a partir de la tipología de problemas multiplicativos. Las acciones que el estudiante realiza para elegir el tipo de problema, en las etapas  de comprender y planear, dan cuenta del proceso metacognitivo de planificación. Las acciones que realiza al implementar los procedimientos correspondientes, la vigilancia de la coherencia entre las etapas de comprender, planear y ejecutar, son evidencia del proceso metacog- nitivo de control. Finalmente, las acciones que realiza para verificar, hacen observable el proceso metacognitivo de evaluación.

Adicional a la implementación de la estrategia general, presentamos cada uno de los tipos de problemas multiplicativos propuestos en el marco teórico. Luego, los estudiantes identificaron las relaciones entre las magnitudes involucradas en el problema, las representaciones gráficas, las operaciones y las estrategias de verificación acordes a cada tipo de problema (Ilustraciones 4 y 5).

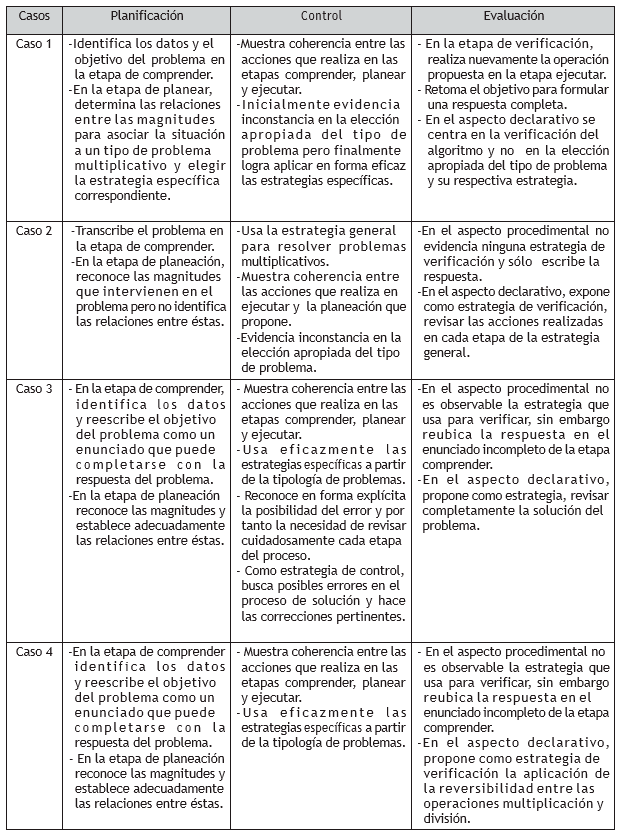
Para atender a los objetivos hicimos un análisis de contenido de los instrumentos 1 al 5 aplicados a cuatro estudiantes. Presentamos en la tabla 2, las descripciones de las estrategias específicas de los estudiantes a partir de las categorías de análisis.

Conclusiones y proyecciones

Con respecto al primer objetivo general, podemos concluir que se logró puesto que implementamos una estrategia metacognitiva general, producto del análisis de los elementos teóricos, que permitió hacer observables los procesos metacognitivos en las etapas correspondientes.

En relación con el segundo objetivo general, logramos describir las estrategias metacognitivas específicas que usan los estudiantes con base en los procesos metacognitivos propuestos por Flavell (1979), mediante la aplicación de la estrategia general.

Ilustración 4. Ejemplo de implementación de la tipología de problemas multiplicativos. Instrumento 3. Caso 3.

Ilustración 5. Evaluación estrategia general y tipología. Instrumento 4. Caso 1.

De acuerdo con las descripciones de las estrategias metacognitivas específicas de cada uno de los casos, podemos deducir que la aplicación de la estrategia metacognitiva general contribuyó al mejoramiento de los procesos de enseñanza y de aprendizaje de la solución de problemas multiplicativos puesto que, por una parte, permitió al docente evaluar la competencia metacognitiva a través de indicadores asociados con la planeación de una estrategia de solución, la permanente revisión de los procedimientos y la verificación de la solución de los problemas. Por otra parte, permitió a los estudiantes hacer conciencia de la importancia de la aplicación de la estrategia general para dirigir sus acciones en la solución de problemas.

Como proyección de esta investigación, consideramos necesario que en el  plan de estudios de matemáticas de los primeros grados de la primaria del Gimnasio Campestre, se incluyan herramientas cognitivas que contribuyan al proceso de verificación en la solución de problemas multiplicativos, como la estimación, el cálculo mental y la aproximación.

Adicionalmente, en los demás grados es conveniente fomentar en los estudiantes el análisis de diferentes estrategias de so- lución a un mismo problema, que les sirva como medio de verificación e implementar estrategias metacognitivas generales en la enseñanza de otros conceptos de las matemáticas escolares, al igual que una tipología de problemas asociados al concepto como un recurso cognitivo que el estudiante puede usar, para construir sus estrategias metacognitivas específicas.

Así mismo, es necesario trabajar con los estudiantes en todos los grados, para que inicialmente haya una regulación o control externo, guiado por medio de preguntas y estrategias para que más adelante se con- vierta en una regulación interna guiada por los recursos cognitivos y por estrategias adquiridas desde grados anteriores aplicadas de forma autónoma.

Tabla 2. Descripción de las estrategias metacognitivas a partir de las categorías de análisis.

Bibliografía

Almenara, J. y Loscertales, F. (2002). Elaboración de un sistema categorial de análisis de contenido para analizar la imagen del profesor y la enseñanza en la prensa. Universidad de Sevilla.
Ayala (1997). La enseñanza y el aprendizaje de las matemáticas elementales. Cepe. Madrid.
Castro, E.(S.F.)  La resolución de problemas desde la investigación en educación matemática. Departamento de Didáctica de la Matemática. Universidad de Granada.
Fragoso, A. (2.004). Investigación y práctica en la educación de personas adultas, pags. 41-60
Flavell, J (1996). El desarrollo cognitivo. España: Prentice Hall.
Gusmao, J. Algunos matices de estrategias cognitivas-metacognitivas durante resolución de problemas con estudiantes de E.S.O. Boletín das ciencias, Año 17, N°.56, 2004 (Ejemplar dedicado a: XVII Congreso Enciga), pags. 41-42
Guerrero, L. (S.F.) Metacognición y solución de problemas. Recuperado el 3 de octubre de 2008 de www.pedagogica.edu.co/proyectos/semillero/ articulos/articulo13.pdf
Hernández, O. (2002) Procesos cognoscitivos y metacognoscitivos en la solución de problemas matemáticos. Focus I, 2. p.p. 59-72.
López, J. Estrategias metacognitivas en la resolución de problemas matemáticos. Recuperado el 11 de noviembre de 2.008 de http://www.saber.ula. ve/bitstream/123456789/20281/1/articulo15.htm
Ministerio de Educación Nacional (1998). Matemáticas. Lineamientos curriculares. Serie Lineamientos Curriculares. Dirección general de Investigación y desarrollo pedagógico.
Pozo, J.I., Monereo,C.(2002). El aprendizaje estratégico: enseñar a aprender desde el curriculo. Aula XXI, Santillana, Madrid.

Este documento fue tomado de www.revistaelastrolabio.com