Usted está aquí
Metodología POLYA en resolución de problemas
Aplicación de procesos metacognitivos en la resolución de problemas en la estructura aditiva con números enteros en estudiantes de quinto grado
Autores
Sandra Carolina Caipa
Profesor Departamento de Matemáticas Gimnasio Campestre
[email protected]
Wilson E. Torres Sánchez
Profesor Departamento de Matemáticas Gimnasio Campestre
[email protected]
Resumen
La presente investigación buscó determinar los procesos metacognitivos aplicados por los estudiantes de grado quinto de un colegio de la ciudad de Bogotá, al solucionar problemas de la estructura aditiva con números enteros. El trabajo de campo se basó en la técnica de resolución de problemas planteada por el matemático George Polya y los análisis se realizaron a nivel cualitativo. El estudio concluye que los estudiantes mejoraron sus procesos metacognitivos lo que permitió ordenar sus procesos, en particular el cuarto pasó de la metodología que se refiere al look back (mirar hacia atrás), donde los estudiantes reflexionaron sobre su propio aprendizaje y propusieron soluciones alternas al problema. De esta forma, los estudiantes fueron quienes asumieron el control de su aprendizaje a través de un proceso netamente metacognitivo.
Introducción
La resolución de problemas es una habiidad básica para la vida, que implica un pensamiento crítico, y lleva al individuo a la planeación de unas estrategias para alcanzar una meta (Keller, 1998). Según el National Council of Teachers of Mathematics (NTCM), la resolución de problemas juega un papel importante en la comprensión de las matemáticas, resolver un problema significa un reto intelectual para los estudiantes.
Por otra parte, la metacognición es vista como “un conjunto de conocimientos, habilidades y actitudes que el estudiantes debe poner en práctica para un continuo autoexamen, autocontrol, autorregulación y autocorrección de su pensamiento” (Modelo Pedagógico Gim- nasio Campestre, 2013). Así mismo, ésta exige procesos de evaluación y autoevaluación diferentes que correspondan a la naturaleza propia y enseñable de esta competencia. Sin embargo, procesos como: la auto-regulación, planeación y monitoreo que se relacionan con la metacognición no son percibidos por una parte de los estudiantes como habilida- des intrínsecas al aprendizaje de las ma- temáticas, estas son necesarias dentro del proceso de resolución de problemas.
En ese orden de ideas, si se ponen juntos el concepto de resolución de problemas, como una habilidad para la vida, y la metacognición, como un proceso que puede “contribuir a mejorar la manera de cómo afrontar el mundo” (Woods 1998, p.87 en Modelo Pedagógico Gimnasio Campestre, p.19), el proceso de enseñanza aprendizaje se complejiza aún más. Es por ello que se hace necesario buscar estrategias que ayuden a los estudiantes a tener una mejor aplicación de sus procesos metacognitivos en la resolución de problemas. Particularmente, en quinto grado se pretende equilibrar las rutinas y habilidades que les permitan a los estudiantes desempeñarse efectivamente en su vida escolar. Por lo tanto, “la apropiación de procesos de monitoreo y control en la resolución de problemas podría garantizar una motivación intrínseca que le permita a los estudiantes ser flexibles y adaptarse a las exigencias actuales” (Modelo Pedagógico Gimnasio Campestre, p.19).
Teniendo en cuenta lo anterior, surge la pregunta de investigación ¿Cuáles son los procesos metacognitivos aplicados por los estudiantes de grado quinto A de un colegio masculino al solucionar problemas de la estructura aditiva con números enteros? Los objetivos de este trabajo investigativo fueron determinar los procesos metacognitivos aplicados por los estudiantes de grado quinto A al solucionar problemas de la estructura aditiva con números enteros; identificar dificultades en los estudiantes de quinto A en los pasos para la resolución de problemas de la estructura aditiva con números enteros; construir un modelo de seguimiento de procesos metacognitivos en los estudiantes de quinto A en la resolución de problemas de la estructura aditiva con números enteros; y analizar las diferentes formas de ejecución del modelo de seguimiento de procesos metacognitivos desarrollados por los estudiantes de quinto A en la resolución de problemas de la estructura aditiva con números enteros.
La resolución de problemas
Definición de problema
Un problema es una situación que ubica a quien lo resuelve ante la necesidad de desplegar su actividad cognitiva en un intento de búsqueda de estrategias, de elaboración de conjeturas y toma de decisiones (Azcue, Diez, Lucanera et al., 2006). En términos generales, “un problema surge cuando existen obstáculos entre una situación dada y la situación a la que se quiere llegar, es querer encontrar un camino para poder llegar del estado actual al estado final, o al que se quiere obtener” (Torres, 2011, P. 64). El poder ayudar a que los estudiantes resuelvan problemas debe ser una de las tareas más importantes del docente de matemáticas. En ese orden de ideas, el docente debe buscar estrategias para que los estudiantes resuelvan problemas en diferentes contextos. Con el enfoque del Modelo Pedagógico del Colegio se pretende que los estudiantes resuelvan problemas a partir del desarrollo de sus competencias.
Pasos para resolver problemas
Según Ballestero (2002) la solución de problemas es un complejo constructo, que cumple el doble y poderoso papel de aliado y/o enemigo en materia de enseñanza, ya que interfiere directamente en los procesos de enseñanza-aprendizaje, y por tanto en los niveles de desarrollo alcanzados por el alumno. Generalmente, para resolver un problema se necesitan de una serie de pasos o procedimientos heurísticos que, así sea inconscientemente, un individuo debe tener en cuenta para llegar a la posible solución del mismo (Torres, 2013).
Para los propósitos de este estudio se usará como referencia el método de cuatro pasos para resolver problemas formulados por George Polya (1945). De acuerdo con este autor los pasos son: 1. Entender el problema., 2. Configurar un plan, 3. Ejecutar el plan, y 4. Examinar la solución.
1. Entender el problema: se refiere a que el estudiante pueda responderse una serie de preguntas como ¿Entiendo todo lo que dice el problema?, ¿Puedo replantear el problema con mis propias palabras?, ¿Cuáles son los datos que hacen parte del problema?, ¿Sé a dónde quiere llegar?, ¿Hay suficiente información?, ¿Hay información que no es clara?, ¿Es este problema similar a algún otro que ya haya resuelto antes?
2. Configurar el plan: se refiere al cómo o qué estrategia va a usar el estudiante para resolver el problema. Las estrategias pueden partir desde aplicar pruebas de ensayo y error, hasta plantear toda una táctica que le permita intentar llegar a la solución del mismo.
3. Ejecutar el plan: se refiere a la puesta en práctica de lo que el estudiante estableció en la configuración. Es llevar a cabo una a una las etapas planteadas. En este punto puede suceder que en un momento determinado lo que se planteó no sea pertinente para la solución del problema, razón por la cual hay que replantear la estrategia y volver a comenzar. Generalmente en la ejecución se usan procesos matemáticos que permitan darle la exactitud que requiere la solución del problema.
4. Examinar la solución: se refiere al poderse cuestionar sobre lo que se hizo, ver si el proceso desarrollado permitió en realidad resolver el problema. En este paso el estudiante debe acudir a sus procesos metacognitivos para revisar si lo que hizo está bien o está mal y, si es necesario, replantear el proceso de resolución.
Metacongnición
Para Rodríguez (2005), el concepto de metacognición es muy complejo y reciente en la educación. Dicho constructo se comenzó a trabajar en procesos de investigación desde la psicología por la década de los setenta del siglo pasado. La metacognición se ha enmarcado dentro de los procesos cognitivos en los últimos años y, de acuerdo a Silva (2006), la metacognición desde la investigación indaga sobre cómo los seres humanos piensan y controlan sus propios procesos de pensamiento. Curotto (2010), refiriendo a Flavell (1976), comenta que la metacognición es el conocimiento sobre los propios procesos y productos cognitivos y el mismo conocimiento sobre las propiedades de la información, datos relacionados con el aprendizaje y cualquier aspecto sobre los productos cognitivos.
Por su parte, Silva (2006) considera que la metacognición tiene dos clasificaciones y a su vez la primera clasificación se puede asociar a dos componentes: el conocimiento sobre los procesos cognitivos y la regulación sobre esos mismos procesos cognitivos. El conocimiento, a su vez, se encasilla en tres aspectos: el conocimiento sobre el sujeto, sobre las tareas y sobre las estrategias. De esta forma, lo metacognitivo se puede encasillar al conocimiento de la amplitud de la memoria ante tópicos relacionados al conocimiento sobre la complejidad de las tareas, en donde se establecen jerarquías y se determinan estrategias para aprendizajes particulares. El segundo componente se refiere a procesos que permiten regular los procesos metacognitivos. Por una parte la planificación, actividad que debe ser previa al desarrollo de cualquier tarea y que según Silva (2006) requiere el diseño de una heurística para prever el camino de las acciones y estrategias a seguir. Por otra parte, la actividad establecida en el momento que se comienzan a ejecutar las acciones, y se traducen a partir de la verificación, recomposición y revisión de la estrategia empleada. Por último la evaluación es la que permite constrastar los resultados con los objetivos planteados.
La segunda clasificación que establece Silva (2006) se refiere a dos líneas de investigación: el monitoreo y el control congnitivo. El monitoreo se refiere a los procesos de pensamiento y los estados de conocimiento que hacen parte del individuo. El control metacognitivo es definidio como la volutad para dirigir los propios procesos de pensamiento y la recuperación de la memoria. El control combinado con el monitoreo determinan la planeación y asignación del tiempo al estudio, el uso de estrategias de aprendizaje y el tiempo necesario para recuperar alguna información de la memoria. En ese orden de ideas, Silva (2006) analiza como los procesos metacognitivos de los estudiantes afectan los procesos de aprendizaje de las matemáticas:
La metacognición es entendida como un componente del sistema ejecutivo de la inteligencia: nos referiremos al conocimiento introspectivo sobre el estado de cognición y su operación la conciencia de lo que uno sabe sobre la manera de cómo lo sabe. Es por ello que la función de la metacognición es dar forma y regular las rutinas y estrategias cognitivas (p.81)
Silva (2006) también menciona cómo a medida que la conciencia sobre lo que está aprendiendo aumenta la actitud frente al conocimiento es más favorable. Finalmente, este autor afirma que “el aprendizaje es el resultado de una acción voluntaria por parte de quien aprende”, (p.90) lo que significa que a mayor conciencia mejor la calidad de lo que se aprende.
Así mismo, el Modelo Pedagógico del Gimnasio Campestre establece la metacognición como una de las cuatro competencias que se enseñan, aprenden y evalúan de manera universal en todos los grados y asignaturas y se caracteriza a partir de cuatro fases: apropiación de la meta, planificación de estrategias, desarrollo cognitivo y producto y evaluación. Estas fases hacen parte de un ciclo, que puede desarrollarse las veces que sea necesario y exigiendo cada vez más dificultad. En la figura 1 se observa la interrelación de las fases de la metacognición desde el Modelo Pedagógico del Gimnasio Campestre (2013).
Teniendo en cuenta lo anterior se pudo establecer una relación entre la metodología de Polya para la resolución de problemas y lo establecido desde la competencia de la metacognición en el Modelo Pedagógico del Gimnasio pestre a partir de los cuatro pasos que cada una maneja (tabla 1).
Materiales y métodos
El enfoque de la investigación fue de carácter cualitativo interpretativo y el tipo de investigación fue estudio de caso. La técnica de recolección de la información fue la videoscopía y las transcripciones, así como la creación de matrices de análisis que permitieran realizar el seguimiento del proceso de resolución de problemas de cada uno de los estudiantes, basados en la metodología propuesta por el matemático húngaro George Polya. Finalmente se realizaron entrevistas, una antes y otra después del trabajo de campo, a la docente que desarrolló el trabajo de campo. La unidad de análisis utilizada fue la sinopsis a partir de cuatro sesiones de clase de 45 minutos cada una.
La población escogida fueron estudiantes de grado quinto en edades entre 11 y 12 años del Gimnasio Campestre y la muestra fue un total 25 estudiantes.
Descripción y Análisis de Resultados
En el salón de clases se llevaron a cabo cuatro sesiones donde el objetivo principal fue resolver problemas de carácter matemático relacionado con la estructura aditiva de números enteros. Mediante esta actividad se buscó identificar los momentos de institucionalización de los procesos metacognitivos basándose en la estructura propuesta por George Polya y a su vez observar los procesos que usaron los estudiantes. Las clases fueron desarrolladas totalmente en inglés[1]. Se incluye una descripción de las sesiones.
Sesión 1: Para comenzar la sesión, la docente organizó a los estudiantes en grupos de tres para que resolvieran un problema relacionado con la estructura aditiva de números enteros que requería más de un paso para resolverlo. La docente no explicitó que estrategia usar, ni asesoró el proceso. El tiempo dado para el desarrollo de la tarea asignada a los grupos fue de 45 minutos. A continuación se observa una transcripción a partir del video que se hizo del proceso:
Teacher: solve in the way you consider… in the case you can´t solve it explain why you could not.
T: what we are going to do to try to collect information about this activity… share the strategies you used
Student1: T-charts, normal operations (algorithms)
S2: Number lines… variables…
S3: Notebooks, key words, equations, multiple operations
S4: simple operations, flowcharts
S5: Mental math
S6: Drawings
S1: Si ve es imposible...
S2: Hágalo con decimales… esta es una de las operaciones que usamos…
S3: which is april…
S4: yes… put here and try again
S3: but it is not here
S5: en april
S6:pero no es el mismo.. ahhh es que son dos meses… toca hacer dos…
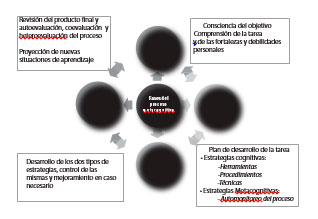
Figura 1. Fases del proceso metacognitivo según el Modelo Pedagógico del Gimnasio Campestre (2013 p.19)
Tabla 1. Paralelo entre los pasos de la metodología Polya y las fases del proceso metacognitivo del Modelo Pedagógico del Gimnasio Campestre.


Estudiantes trabajando en la sesión 1 con sus estrategias metacognitivas. Foto: Gimnasio Campestre.
Sesión 2: En esta sesión se explicó sobre la metodología de solución de problemas establecida por George Polya. Cada paso se comparó desde el contexto matemático, pero también se utilizaron ejemplos de la vida cotidiana. Fotografías 3 y 4: la docente explicando la metodología de resolución de problemas creada por George Polya.
Sesión 3: En esta tercera sesión se les dio a los estudiantes un problema relacionado a la estructura aditiva, usando un formato en donde se especificaban los pasos de resolución de problemas, de acuerdo a la metodología de Polya.
Cada paso tenía preguntas anexas que guiaron el proceso de reflexión de los estudiantes, haciendo un énfasis especial en el último paso donde ellos debían revisar su proceso y proponer una solución diferente a la que dieron inicialmente. A continuación, se observa la transcripción del trabajo de la profesora con algunos estudiantes:
Teacher: Who remembers the Polya’s steps?
T: How many steps? Group: Four…
Student 1: Understand the problem
S2: think plan
S3: carry out the plan
S4: look back
T: Solve the problem following the
Polya’s steps
 En esta sesión, cuando los estudiantes estaban resolviendo el problema usando los pasos de Polya encontraron dificultades al desarrollar el cuarto paso (look back). No estaban seguros sobre la manera de llevar a cabo este proceso, por tal razón la docente hizo un pare en la clase para explicarlo nuevamente y aclarar sus dudas. Aspectos de la interacción en este momento se observan en la siguiente transcripción:
En esta sesión, cuando los estudiantes estaban resolviendo el problema usando los pasos de Polya encontraron dificultades al desarrollar el cuarto paso (look back). No estaban seguros sobre la manera de llevar a cabo este proceso, por tal razón la docente hizo un pare en la clase para explicarlo nuevamente y aclarar sus dudas. Aspectos de la interacción en este momento se observan en la siguiente transcripción:
Student 1: take away and subtract the numbers one by one
Teacher: Now explain an alternative solution.
En este momento el profesor ayuda a los estudiantes a redactar sus ideas.
T: What is metacognition?
S1: Metacognition is to show we check our process in a critical thinking of our- selves.
T: Checking our own process…self moni toring.
S2: It is in our own process of learning... correct the…the mistakes you have… in our process of understanding math.
T:..Do you think is only in math? Group: No
T:.. any topic…
S3: … metacognition is evaluation of the process of learning…

Estudiantes trabajando en la resolución de un problema de acuerdo a la metodología Polya e interactuando en clase con la docente. Foto: Gimnasio Campestre.
Sesión 4: En esta sesión los estudiantes evaluaron junto con la docente el impacto que tuvo el conocer la estrategia en la solución de problemas que propuso Polya en su desempeño y solución del problema. Así mismo, analizaron el efecto que tuvieron las estrategias metacognitivas usadas por ellos en sus resultados, esto se evidencia en la siguiente transcripción:
T: Do you think Polya’s method help you in your metacognition process?
S4: The Polya’s method helps me to metacognition... because in understanding the problem… we look the problem… and the look back part is then.. look is the process to help you to improve the problem.
T: Dou you think a person who does not know Polya’s method would do metacognition?
Group: NO
S5: It’s possible.. because when we are small we can do metacognition..
S6: .. Maybe.. there are ways to solve the problem.. one way using Polya´s method and the other is maybe… doing his own method..
S7:... I think it is very useful because… when you have plan you could solve the problem..
S8:... it is useful…we could use it for life..
S9:…It is a way to prepare us for life…
T: When you use the Polya’s method who has the control of the processes?
Group: Ourselves
En la figura 2 se analizan las estrategias metacognitivas utilizadas por una pareja de estudiantes antes de aplicar la metodología Polya. Como se puede observar algunas estrategias no son del todo metacognitivas, son más bien cognitivas, como proponer una ecuación o hábitos de cómo usar el cuaderno.




En este caso la estrategia usada por el estudiante es una lista de chequeo con tres recursos:
- Usar el cuaderno
- Discutir en grupo
- Proponer una ecuación para solucionar el problema.
En este caso se usa una estructura de monitoreo de la solución de problemas y se evidencia en los títulos de “Steps & answer”:
También se usó la recta numérica como estrategia de solución numérica. De igual forma plantearon una ecuación e hicieron un diagrama.
Revisando las figuras 2 y 3 se observa el uso de estrategias cognitivas mezcladas con metacognitivas. Los estudiantes no establecen diferencia entre las unas y las otras.
Este grupo hace uso de ecuaciones y diagramas como estrategia para la solución del problema.
En la figura 4, a pesar de no resolver el problema, los estudiantes intentan utilizar estrategias de solución cognitivas. Sin embargo, en su análisis se observan procesos metacognitivos del por qué no llegaron a la solución.
En la figura 5 se observa la solución del problema dada por el estudiante utilizando la metodología Polya, en esta se evidencian de mejor forma los procesos metacognitivos en la cuarta parte, el “Look Back”.
En este caso ya se les había explicado los pasos de Polya y el estudiante fue más descriptivo y buscaba reflexionar sobre su propio proceso usando como guía las preguntas que se le dieron. También se ve una secuenciación más clara. En la última parte sobre “look back” propone un resultado alterno para resolver el mismo problema.
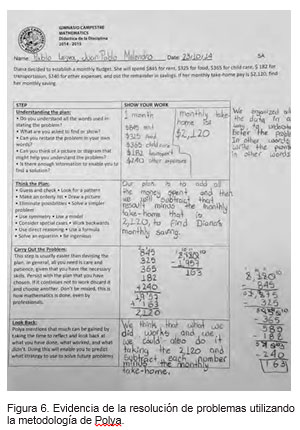
En la figura 6 se observa que los dos estudiantes aplicaron procesos metacognitivos en el proceso de resolución del problema, utilizando la reflexión en cada uno de los momentos desarrollados y evidenciando su proceso de pensamiento y buscado una solución alternativa para el mismo problema.
La tabla 2 presenta las apreciaciones sobre las estrategias metacognitivas utilizadas por los estudiantes en la resolución de problemas de la estructura aditiva con números enteros, se presenta un paralelo entre dichas estrategias con el antes y el después de la explicación de la metodología Polya.
Tabla 2. Paralelo de estrategias utilizadas por los estudiantes en la resolución de problemas
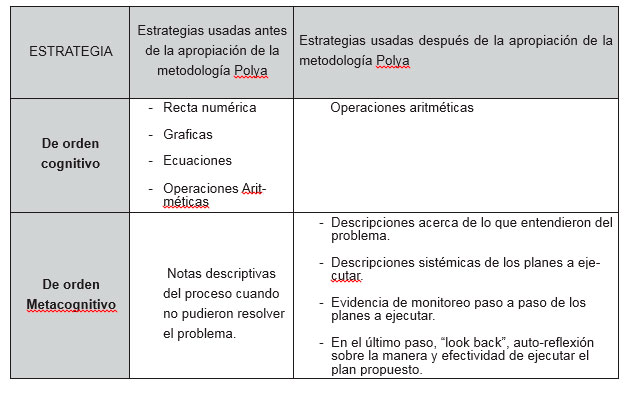
 Como se observa en la tabla 2, se percibe un avance de estrategias metacognitivas utilizadas por los estudiantes, que evidenció claridad en la resolución de problemas después de apropiar la metodología Polya y mostrar de mejor manera los procesos metacognitivos empleados en el proceso. Lo que muestra el proceso es que, independiente de la solución o no del problema, los estudiantes tuvieron más claridad al utilizar la metodología propuesta una vez que la conocieron y de plantear estrategias para la solución y el monitoreo del proceso de solución.
Como se observa en la tabla 2, se percibe un avance de estrategias metacognitivas utilizadas por los estudiantes, que evidenció claridad en la resolución de problemas después de apropiar la metodología Polya y mostrar de mejor manera los procesos metacognitivos empleados en el proceso. Lo que muestra el proceso es que, independiente de la solución o no del problema, los estudiantes tuvieron más claridad al utilizar la metodología propuesta una vez que la conocieron y de plantear estrategias para la solución y el monitoreo del proceso de solución.
Discusión y conclusiones
Se pudieron evidenciar las estrategias (tabla 2) utilizadas por los estudiantes antes y después de la aplicación del modelo de resolución de problemas a partir de la metodología de George Polya, dando así respuesta a la pregunta de esta investigación.
Ahora, respecto a la identificación de las dificultades en los estudiantes de quinto A en los pasos para la resolución de problemas de la estructura aditiva con números enteros, las mismas se evidencian en aspectos como el que una lista de estrategias de resolución que ellos conocían, tales como entender el problema, hacer un plan, ejecutarlo y revisar el proceso desarrollado, no fue aplicada adecuadamente al contexto planteado de acuerdo al problema. También se observó que no hubo evidencia de procesos de monitoreo y verificación, que son claves al desarrollar proceso metacognitivos. De igual forma, se evidenció una falta de conexión entre los procesos metacognitivos y su aplicación a la resolución de problemas. Los estudiantes simplemente separaban el con- cepto de metacognición como un simple ejercicio de corregir errores y no como un proceso cíclico de retroalimentación que pudiera ayudarlos con miras a evitar futuros errores.
Respecto al modelo de seguimiento de los proceso metacognitivos de acuerdo a la metodología planteada por George Polya, el mismo se aplicó y arrojó mejora en cuanto a las estrategias metacognitivas utilizadas por los estudiantes en términos de autorreflexión de los pasos seguidos, así como soluciones alternas al problema planteado. Sin embargo, pudieron hacer falta más sesiones para afianzar dicho modelo, en especial cuando se plantean preguntas reflexivas para guiar los pasos de resolución. Lo anterior se podría mejorar en otro momento de aplicación del proceso metodológico planteado en la investigación.
Por otra parte, al analizar las diferentes formas de ejecución del modelo de seguimiento de procesos metacognitivos desarrollados por los estudiantes, se observaron dos maneras de asumir este modelo. La primera se relaciona con aquellos estudiantes que son más descriptivos en sus procesos y que tienen en cuenta todos los detalles que los llevaron a la resolución de su problema, haciendo sus procesos metacognitivos más elabo- rados y específicos. La segunda se refiere a aquellos estudiantes que necesitan trabajar en sus autorreflexiones, ya que proveen evidencias suficientes de cómo la autorreflexión los puede ayudar en la resolución de un problema.
El impacto general de esta intervención es analizado desde tres momentos específicos. El primero, se refiere a los procesos metacognitivos que los estudiantes aplicaron en la solución de problemas. En segundo lugar se aborda el efecto que esta investigación tuvo en el que hacer docente de la profesora de matemáticas. Y por último, la reflexión sobre como un modelo propio de la didáctica de las ma- temáticas en esta caso la Metodología de George Polya, puede convertirse en una herramienta para mejorar los procesos metacognitivos de los estudiantes.
En cuanto a los procesos metacognitvos que los estudiantes aplicaron en la solución de problemas, se puede concluir que es fundamental crear espacios dentro de la planeación donde la metacognición sea enseñada a través de una estruc- tura tangible que pueda ser practicada por los estudiantes en la vida diaria. De esta manera, la metacognición adquie- re un carácter enseñable y evaluable. Lo anterior lo refuerza Curotto (2010), quien menciona que la formulación de preguntas, por parte del estudiante, es un recurso de “autorregulación cogniti- va” que le permite controlar su propio estado de comprensión. En relación al efecto que esta investigación tuvo en el quehacer docente, se puede concluir que estos espacios de observación, reflexión e institucionalización de un proceso en específico, en este caso metacognición en la resolución de problemas desde la metodología de Polya, enriquecen la práctica diaria y aportan una estructura que permite ver más de cerca los pro- cesos que desarrollan los estudiantes.
De acuerdo a como lo dice Brousseau (2005) entender no siempre es condición suficiente para aprender.
Esta experiencia provee al docente con herramientas para empoderar a los estudiantes en su aprendizaje desde la autoreflexión las cuales pueden ser aplicables a cualquier espacio de la vida. Así mismo, cuando un estudiante reflexiona sobre cómo resolver un problema o cómo lo ha resuelto en matemáticas puede ampliar el espectro de esta habilidad y transferirlo en la solución de cualquier problema de su vida diaria.
Finalmente, la aplicación de la metodología de Polya en la solución de problemas dentro de un marco metacognitivo le permitió a los estudiantes estructurar su pensamiento y guiar los procesos de auto-reflexión de una manera más ordenada. Esta metodología es muy favorable para este tipo de competencia ya que en el último paso invita a los estudiantes a revisar su proceso y buscar soluciones alternas, es aquí donde el estudiante tendría que enfatizar en sus proceso metacognitivos.
Para futuras investigaciones de este orden sería importante profundizar más en estrategias metodológicas que sirvan para que los estudiantes ajusten sus procesos metacognitivos al momento de solucionar problemas.
Lista de referencias
Alagia, H, Bressan, A y Sadovsky P, (2005). Formación Docente Matemática, Reflexiones Teóricas Para La Educación Matemática. Buenos Aires.
El Zorzal. Recuperado de http://books.google. com.co/books
Azcue, M., Diez, M. L., Lucanera, V., Scandroli, N., (Agosto de 2002). Resolución de un problema complejo utilizando un elemento de naturaleza heurística. Facultad de Ciencias Veterinarias de la Universidad Nacional del Centro de la Provincia de Buenos Aires, Argentina. Número 37/6, 10-2-06.
Ballestero, S, (2002). Resolución de problemas y motivación en espacios virtuales. Propuesta de una línea de investigación. Universidad de Salamanca.
Brousseau, G, (1999). Educación y Didáctica de las Matemáticas. En Educación Matemática (prensa). Nov. México. Discurso.
Brousseau, G y Gibel, P, (2005). Didactical Handling of Students’ Reasoning Processes in Problem Solving Situations. Recuperado de link.springer. com/article
Brousseau, G, (2007). Formación Docente Matemática, Iniciación al Estudio de la Teoría de las situaciones Didácticas. Traducción Dilma Fregona. Recuperado de books.google.com.co/boo ks
Codina, A, (2000). Elementos para una Reflexión acerca del Uso de la Computadora en el Aprendizaje de Estudiantes de Bachillerato Vía Resolución de Problemas. Tesis para obtener el grado de Maestro en Ciencias en la Especialidad Matemática Educativa. Universidad de Granada Departamento de Didáctica de la Matemática. México DF.
Curotto, M, (Noviembre de 2010) La Metacognición en el Aprendizaje de la Matemática. Revista Electrónica Iberoamericana de Educación en Ciencias y Tecnología. Volumen, Número 2.
Chavarria, J, (2006). Teoría de las Situaciones Didácticas. Escuela de Matemática. Universidad Nacional. Texto Recupeado de http://mc142.uib. es:8080/rid=1K14VDFDF-1Z40Y57-8PG/10-55-1-PB. pdf.
Gimnasio Campestre (2013). Modelo Pedagógico. Bogotá, Colombia.
Guerrero F, Sanchez, N y Lurduy O, (2006). La Práctica Docente Apartir Del Modelo DECA y La Teoria De Las Situaciones Didácticas. V Festival Internacoinal
De La Matemática De Costa a Costa. Matemática Como Lenguaje Para Interpretar Nuestro Entorno. 29 al 31 de Marzo. Recuperado de http://www.cien- tec.or.cr/matematica/pdf/P-Fernando-Gerrero.pdf
Keller, Robert y Concannon T, (1998). Teaching problem-Solving Skills. Center for Teaching and Learning. University of North Carolina at Chapel Hill, CTL Number 20.
Oñorbe de Torre, A., y Sánchez J. M, (1996). Dificultades en la enseñanza-aprendizaje de los problemas de Física y Química. I. Opiniones de los alumnos, en Enseñanza de las Ciencias, 14 (2), pp. 165 - 170.
Rodriguez,E, (2005). Metacognición, Resolución de Problemas y Enseñanza de las Matemáticas. Una propuesta integradora desde el enfoque antropológico. Memoria presentada para optar al grado de doctora. Universidad Complutense. Madrid, España. 2005.
Silva, C, (2006). Eduación en Matemática y Procesos Metacognitivos en el Aprendizaje. Red de Revistas Científicas de America Latina, El Cariba, España y Portugal. Sistema de Informacion Científica. Universidad La Salle, Vol 7. Num. 26 Julio-Diciembre.
Stanic, G. y Kilpatrick, J, (1989). Historical perspectives on problem solving in the mathematics curriculum. In: R. Charles y Silver (Eds.) The teaching and assesing of mathematical problem solving, pp.1-22 Reston, VA: National Council of Teachers of Mathematics.
Torres, W, (2013). Incidencia del género en la obtención de metas académicas en estudiantes de grado décimo de dos colegios de la ciudad de Bogotá. Revista El Astrolabio, volumen 12 Número 1. Enero – Junio 2013. Bogotá, Colombia.
Este documento fue tomado de www.revistaelastrolabio.com
[1] Al momento de la trascripción se respetó el idioma de las intervenciones. Formalmente las conversaciones se dieron en inglés pero en ocasiones en la interacción entre estudiantes, hay un cambio al uso de español.
- 92552 lecturas






